平均値、中央値、最頻値の意味とメリデメをドラゴンボールの戦闘力で説明してみた。

皆さんこんにちは。

最近の世の中、統計に関する基本的な知識があるかないかで理解度がぜんぜん違ってくることがあります。

なのですが、あまり統計に関する説明ってないのも事実。

自分から情報を探しにいかないと意外と見つかりません。

仮に見つかっても、なんかちょっと専門的すぎてなあ、って感じのものも多いですね。

そこで、今日はできるだけわかりやすく統計の基礎の基礎について触れようかと。

ただ、普通に説明してもつまんないですし、頭に入らないので、ドラゴンボールを例に使ってみました。

戦闘力を基準に、平均値や中央値、あともうひとつ大事な指標である最頻値について解説します！

スカウター不要！栽培マンでもわかる平均値、中央値、最頻値の出し方

平均値、中央値、最頻値の基本

それでは、まずこの平均値、中央値、最頻値の意味を簡単におさらいしましょう。

まず「平均値」。これはだいじょうぶですよね。
一応説明すると、「全部の数値を足して、データの総数で割ったもの」です。

仮に今、ある部屋にこのメンツがいたとしましょう。戦闘力を計測したら以下のとおりでした。
（数値出典：http://dragonballbp.web.fc2.com/archives/officialbp.html）
※数値には諸説あります。

このとき、平均値は（8000+4000+1500+1200+1200）÷5＝3,180です。

次に中央値。これは、この5人を「順番に並べた場合に真ん中に来る人の数値」なので、
ラディッツさんの1500ということになります。

※ちなみに、データが偶数の場合、中央値は真ん中２つの平均を取ります。

最後の最頻値ですが、これは「データの中で、もっともよく出てくる数値」です。

なので今回、最頻値は栽培マンさんたちの1200となります。

平均値と中央値の使い分け

平均値と中央値はよく似ています。

両方とも「真ん中」を表す値なのでちょっとまぎらわしいですね。

ただ、似て非なるものですので、使い方を間違えるとえらくミスリーディングな結果を招くので要注意です。

さて、先ほどの5人に、突如フリーザ様（戦闘力53万）が加わったらどうなるでしょう？

平均値は（530000+8000+4000+1500+1200+1200）÷6=90,983.333…と急上昇します。

ですがこの数字をこのグループ全体の「真ん中」と言っていいかは疑問ですね。

あとの人たちは別に何もしてないので・・・。

このように、平均値には
「とんでもなくかけ離れた数値が混じると、それに引きずられてしまう」
というデメリットがあります。

一方、中央値はこの場合（4000+1500）÷2＝2750なので、増えてはいますが、そこまで極端なブレとはなっていません。

そのため、極端な数値を排除する上では中央値がいわゆる「真ん中」を見るうえでは向いているといえます。

特にデータ総数が大きくなると有効。

じゃ、全部中央値でいいじゃんと思いたくなりますが、そうともいえません。

この例で、フリーザ様と悟空さんの戦いがヒートアップしてしまったらどうでしょう。
それぞれ、戦闘力が1億2000万、1億5000万まで跳ね上がったとします。
（数値出典：上記に同じ。）

この場合でも、中央値は相変わらずナッパさんとラディッツさんの間、2750です。

にもかかわらず中央値だけをみて、「このグループの戦闘力は変わらない」って言ったら明らかにおかしいですよね？

かたやナメック星を吹っ飛ばす戦いですよ？

最頻値もトリッキー

最頻値も同じように、今回のフリーザ様のような極端な数値は排除されますので、全体としての傾向を見るのに使い勝手がいいものです。

ただし、ある程度数がないと無意味ですし、最悪バラバラな数値のデータだと最頻値も何もありません。

上の例でいえば、栽培マンさんが一人（一匹？）逃げ出したら最頻値は計測不能です。

また、数値ではなく度数分布（一定の範囲を区切って、そこに該当するデータの個数を数える）を使って、

分布が一番多いところを「最頻値」とすることもあります。

ただし問題は、各区間の切り方で最頻値が変わってしまうこと。

例えば、戦闘力を500刻みにした場合、フリーザ様到着時を基準にすると以下のように分布します。

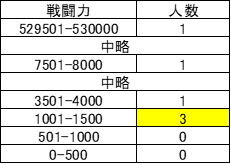
で、最頻値は黄色のところで、数値（人数）は3です。

ところが、戦闘力を1万刻みにすると、分布が

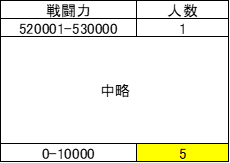
となって、最頻値は5となってしまうのです。同じデータなんですけどねえ。

まとめ

平均値、中央値、最頻値の意味、メリデメをまとめると

となります。戦闘力を語る際の参考にしてみてくださいね笑

本日は以上です。最後までお読みいただきどうもありがとうございました！